Модель Марковица

Страница 2

Материалы » Портфельное инвестирование » Модель Марковица

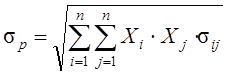(10)

где sp - мера риска портфеля;

sij - ковариация между доходностями i-й и j-й ценных бумаг;

Xi и Xj - доли общего вложения, приходящиеся на i-ю и j-ю ценные бумаги;

n - число ценных бумаг портфеля.

Ковариация доходностей ценных бумаг (sij) равна корреляции между ними, умноженной на произведение их стандартных отклонений:

(11)

где rij - коэффициент корреляции доходностей i-ой и j-ой ценными бумагами;

si, sj - стандартные отклонения доходностей i-ой и j-ой ценных бумаг.

Для i = j ковариация равна дисперсии акции.

Рассматривая теоретически предельный случай, при котором в портфель можно включать бесконечное количество ценных бумаг, дисперсия (мера риска портфеля) асимптотически будет приближаться к среднему значению ковариации.

Графическое

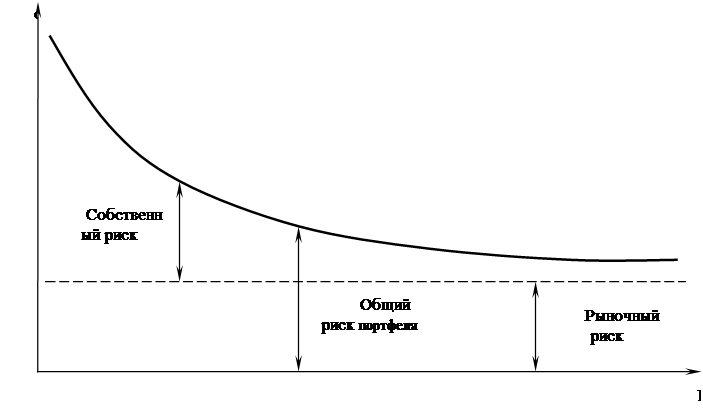представление этого факта представлено на рисунке 2.1.

Рисунок 2.1 - Риск портфеля и диверсификация

Совокупный риск портфеля можно разложить на две составные части: рыночный риск, который нельзя исключить и которому подвержены все ценные бумаги практически в равной степени, и собственный риск, который можно избежать при помощи диверсификации. При этом сумма вложенных средств по всем объектам должна быть равна общему объему инвестиционных вложений, т.е. сумма относительных долей в общем объеме должна равняться единице.

Проблема заключается в численном определении относительных долей акций и облигаций в портфеле, которые наиболее выгодны для владельца. Марковиц ограничивает решение модели тем, что из всего множества "допустимых" портфелей, т.е. удовлетворяющих ограничениям, необходимо выделить те, которые рискованнее, чем другие. При помощи разработанного Марковицем метода критических линий можно выделить неперспективные портфели. Тем самым остаются только эффективные портфели.

Отобранные таким образом портфели объединяют в список, содержащий сведения о процентом составе портфеля из отдельных ценных бумаг, а также о доходе и риске портфелей.

Объяснение того факта, что инвестор должен рассмотреть только подмножество возможных портфелей, содержится в следующей теореме об эффективном множестве: "Инвестор выберет свой оптимальный портфель из множества портфелей, каждый из которых обеспечивает максимальную ожидаемую доходность для некоторого уровня риска и минимальный риск для некоторого значения ожидаемой доходности". Набор портфелей, удовлетворяющих этим двум условиям, называется эффективным множеством.

На рисунке представлены недопустимые, допустимые и эффективные портфели, а также линия эффективного множества.

Рисунок 2.2 - Допустимое и эффективное множества

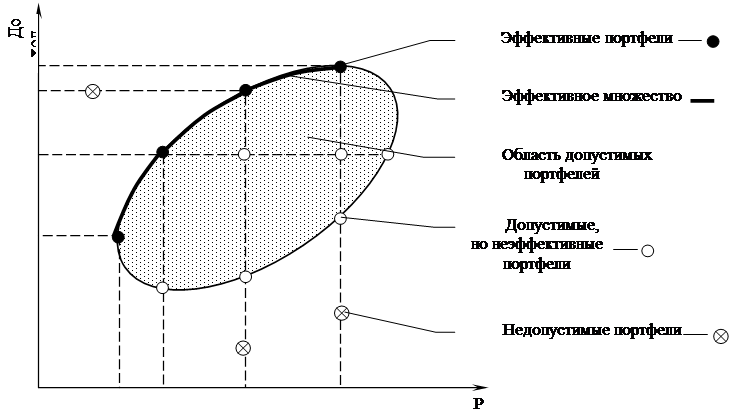В модели Марковица допустимыми являются только стандартные портфели (без коротких позиций). Использую более техническую терминологию, можно сказать, что инвестор по каждому активу находится в длинной позиции. Длинная позиция - это обычно покупка актива с намерением его последующей продажи (закрытие позиции). Такая покупка обычно осуществляется при ожидании повышения цены актива в надежде получить доход от разности цен покупки и продажи.

Из-за недопустимости коротких позиций в модели Марковица на доли ценных бумаг в портфели накладывается условие неотрицательности. Поэтому особенностью этой модели является ограниченность доходности допустимых портфелей, т.к. доходность любого стандартного портфеля не превышает наибольшей доходности активов, из которых он построен.

Рекомендуемое:

Валютные риски и управление ими
Валютные риски являются частью коммерческих рисков, которым подвер­жены участники международных экономических отношений. Валютные риски представляют собой вероятность наступления потерь в результате изменения курса валюты цены (займа) по отношению к валюте платежа в период между подписанием контрак ...

Организационная структура страховой компании
Миссия ЗАО «МАКС»: Мы обеспечиваем жизненную уверенность, стабильность бизнеса и охрану здоровья гражданам России, берем на себя их экономические, имущественные и другие риски. Стратегическая цель - занять лидирующее положение на страховом рынке России. В рамках осуществления миссии и стратегическо ...

Сущность страхового риска
Под риском понимается ситуация, когда зная вероятность каждого возможного исхода, все же нельзя точно предсказать конечный результат. В основе страхования лежит страховой риск. Страховой риск – это неоднозначное понятие, но чаще всего под ним понимается вероятность наступления ущерба. Риск является ...